Matemática e Literatura: INTERVALOS REAIS

O conjunto dos números reais, representado pela letra R, possui vários subconjuntos. Vamos abordar nesta página os subconjuntos que são chamados de intervalos reais, e que são determinados por meio de desigualdades.

Imagine, por exemplo, a infinidade de números reais existentes entre os números 1 e 2. O intervalo pode ser representado de três formas diferentes.

Utilizando colchetes

I = ]1, 2[

Utilizando desigualdades

I = {x∈R | 1<x<2}

Utilizando a reta real

Perceba que representamos o intervalo entre 1 e 2, porém sem incluir esses dois extremos. Neste caso, dizemos que o intervalo é aberto nos extremos 1 e 2.

Agora vamos analisar o intervalo é fechado nos dois extremos):

Utilizando os colchetes

I = [1, 2]

Utilizando as desigualdades

I = {x∈R | 1≤x≤2}

Utilizando a reta real

Observou a diferença? Vamos ver as operações com intervalos reais.

A utilização da reta real na resolução de operações entre conjuntos formados por intervalos reais é muito importante. Através dela é possível observar com mais facilidade as operações de união, interseção e diferença entre conjuntos. Veja o exemplo:

Considere os conjuntos abaixo:

A = ]1, 3]

B = [2, 4[

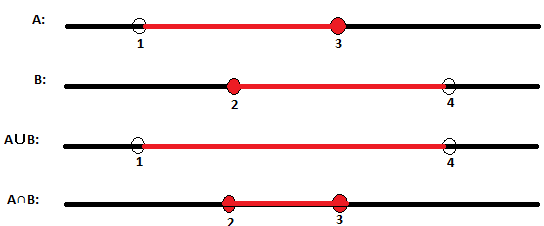
Utilizaremos a reta real para representaremos os intervalos formados pela união e pela interseção de A e B.